
| Homepage Prof. Dr. K. Fritzsche |
| Universität Wuppertal - Fachbereich C |
| Gebäude F, Ebene 12, Zimmer 8 < Tel. (439)-2636 > |
| Gaußstraße 20, 42097 Wuppertal |
Modular
Graphic
Applications
for
TeX
-
The Tutorial
LaTeX stellt schon eine Umgebung zur Verfügung, innerhalb der ganz einfache
Graphiken erstellt werden können.
Als Maßeinheit voreingestellt ist die typografische Einheit Punkt (1pt entspricht etwa 0,35 mm). Der Benutzer kann dies ändern, z.B. mit dem Befehl
Da die Möglichkeiten der Picture-Umgebung sehr eingeschränkt sind, ist MGA-TeX zunächst als Erweiterung der Picture-Umgebung entstanden, hat sich dann aber immer weiter verselbständigt.
Intern (und für den gewöhnlichen Benutzer unsichtbar) steckt immer noch eine Picture-Umgebung mit der Einheit 1pt dahinter.
Um MGA-TeX (in der aktuellen Version 2.4) zu benutzen, muss man die folgenden Style-Files bereitstellen (am besten in dem Ordner, in dem auch das steuernde TeX-File steht):
Als Maßeinheit voreingestellt ist die typografische Einheit Punkt (1pt entspricht etwa 0,35 mm). Der Benutzer kann dies ändern, z.B. mit dem Befehl
\setlength{\unitlength}{1cm}
Danach beziehen sich alle Zahlenangaben auf die Einheit 1 cm. Die Grafik-Umgebung
von LaTeX hat dann die Gestalt
\begin{picture}(Breite ,Höhe )
...
\end{picture}
Da die Möglichkeiten der Picture-Umgebung sehr eingeschränkt sind, ist MGA-TeX zunächst als Erweiterung der Picture-Umgebung entstanden, hat sich dann aber immer weiter verselbständigt.
Intern (und für den gewöhnlichen Benutzer unsichtbar) steckt immer noch eine Picture-Umgebung mit der Einheit 1pt dahinter.
Um MGA-TeX (in der aktuellen Version 2.4) zu benutzen, muss man die folgenden Style-Files bereitstellen (am besten in dem Ordner, in dem auch das steuernde TeX-File steht):
mgtex_24.sty (Kern des Programms mit den Benutzer-Befehlen), mg24_var.sty (Variablen-Deklarationen), mg24_ari.sty (arithmetische Funktionen), mg24_pre.sty (weitere Vorbereitungen), mga_col.sty (Hilfs-Routinen für farbige Darstellungen) mga_ncol.sty (Hilfs-Routinen zur Wandlung von Farbe in Graustufen), mg24_cor.sty (Darstellung von Koordinatenachsen), mg24i_ep.sty und epic.sty (Notfall-Treiber-Interface, falls ps und pdf nicht benutzt werden sollen), mg24i_ps.sty (Treiber-Interface für den Arbeits-Zykel LaTeX-Dvi-Dvips-Ghostview), mg24i_pd.sty (Treiber-Interface für den Arbeits-Zykel PdfLaTeX-Acroread).Für Erweiterungen wie Turtle-Grafik oder 3d-Fähigkeit braucht man außerdem noch
mga_turt.sty, mg24_3d.sty.
Hier ist zunächst einmal eine einfache Zeichnung, entworfen mit der Picture-Umgebung von LaTeX:
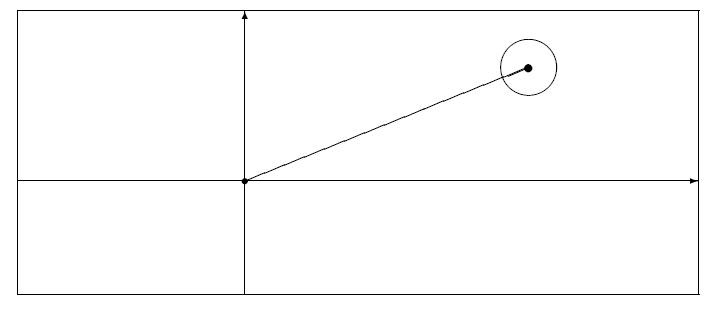
Das Ergebnis ist nicht optimal,
die Syntax in LaTeX etwas schwerfällig:
\setlength{\unitlength}{1cm}
\begin{picture}(12,5)(-4,-2) Breite=12cm, Höhe=5cm, linke untere Ecke bekommt Position (-4,-2)
\put(-4,-2){\framebox(12,5){}} <-- ein Rahmen um die Zeichnung
\put(0,0){\circle*{0.1}} <-- ein dicker Punkt bei (0,0)
\put(0,0){\line(5,2){5}} <-- Gerade von (0,0) nach (5,2)
\put(5,2){\circle*{0.1333}} <-- ein noch dickerer Punkt bei (5,2)
\put(5,2){\circle{1}} <-- Kreis mit Durchmesser 1cm um (5,2)
\put(-4,0){\vector(1,0){12}} <-- Achsenkreuz (x-Achse)
\put(0,-2){\vector(0,1){5}} <-- Achsenkreuz (y-Achse)
\end{picture}
Hinzu kommt das Problem, dass Geraden nur mit bestimmten Steigungen und Kreise nur mit
bestimmten Durchmessern gezeichnet werden können.
In MGA-TeX existieren all die genannten Probleme nicht. Das Ergebnis sieht fast genauso wie in der Picture-Umgebung aus (bis auf die Pfeilspitzen), die Endqualität ist besser.
In MGA-TeX existieren all die genannten Probleme nicht. Das Ergebnis sieht fast genauso wie in der Picture-Umgebung aus (bis auf die Pfeilspitzen), die Endqualität ist besser.
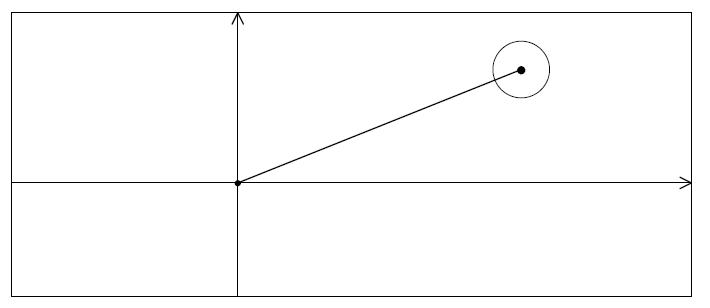
Dazu sollte der LaTeX-Quellcode folgende Befehle enthalten:
\usepackage[ps]{mgtex_24} Option ps für LaTeX,dvips,gsview
... Option pd für PDFLaTeX,acroread
\begin{document}
...
\InitGraph{12}{5}{4}{2}{1cm} Breite, Höhe, Nullpunktkoordinaten, Maßeinheit
\DrawBoundary <-- ein Rahmen um die Zeichnung
\MedPointAt(0,0) <-- ein dicker Punkt bei (0,0)
\LineAt(0,0,5,2) <-- Gerade von (0,0) nach (5,2)
\BigPoint <-- ein noch dickerer Punkt bei (5,2)
\Circle(0.5) <-- Kreis mit Durchmesser 1cm um (5,2)
\Axes <-- Achsenkreuz
\CloseGraph
...
\end{document}
Die Graphik-Umgebung von MGA-TeX besteht also aus dem Befehls-Paar
\InitGraph{Breite}{Hoehe}{x0}{y0}{Masseinheit}
und
CloseGraph.
Innerhalb dieser Umgebung funktionieren im Prinzip auch alle LaTeX-Befehle der Picture-Umgebung,
allerdings mit der Einheit 1pt. Deshalb ist es besser, mit den MGA-TeX-Befehlen zu arbeiten.
MGA-TeX arbeitet mit einem virtuellen Cursor. Der kann mit \MoveTo(a,b) bewusst auf die Position (a,b) gesetzt werden. Nach dem Befehl \LineAt(a,b,c,d) steht der Cursor an der Position (c,d). Von dort aus kann anschließend mit Hilfe des Befehls \LineTo(e,f) eine weitere gerade Linie zum Punkt (e,f) gezeichnet werden.
Die Befehle \Point, \MedPoint und \BigPoint setzen an die aktuelle Cursorposition einen kleinen, mittleren oder dicken Punkt.
Wünscht man eine andere Position (x,y) für den Punkt, so benutzt man die Befehle \PointAt(x,y), \MedPointAt(x,y) und \BigPointAt(x,y). Die gleiche Logik wird beim Zeichnen von Kreisen benutzt. \Circle(r) zeichnet einen Kreis mit Radius r um die aktuelle Cursorposition, \CircleAt(x,y)(r) zeichnet den Kreis um den Punkt (x,y).
MGA-TeX kann aber noch viel mehr! Die nächste Zeichnung soll ein Achsenkreuz und den Graphen der Sinusfunktion enthalten.
Für das Zeichnen der Funktion y=a·sin(bx+c) + d in den Grenzen von u bis v steht der Befehl \Sinus(a,b,c,d)(u,v)[n] zur Verfügung. Die Zahl n bestimmt, aus wie vielen Streckenstücken der Graph zusammengesetzt werden soll.
Für das Zeichnen der gewöhnlichen Sinusfunktion muss also a=1, b=1, c=0 und d=0 gesetzt werden. Will man die Funktion auf dem Intervall [-4,8] zeichnen, so umfasst das 12cm. Die Kurve wird glatt genug, wenn man sie aus 120 Streckenstücken zusammensetzt. Das passt alles in eine Zeichnung von 12×3 cm, der Nullpunkt kann an die Stelle (4,1.5) gesetzt werden.
MGA-TeX arbeitet mit einem virtuellen Cursor. Der kann mit \MoveTo(a,b) bewusst auf die Position (a,b) gesetzt werden. Nach dem Befehl \LineAt(a,b,c,d) steht der Cursor an der Position (c,d). Von dort aus kann anschließend mit Hilfe des Befehls \LineTo(e,f) eine weitere gerade Linie zum Punkt (e,f) gezeichnet werden.
Die Befehle \Point, \MedPoint und \BigPoint setzen an die aktuelle Cursorposition einen kleinen, mittleren oder dicken Punkt.
Wünscht man eine andere Position (x,y) für den Punkt, so benutzt man die Befehle \PointAt(x,y), \MedPointAt(x,y) und \BigPointAt(x,y). Die gleiche Logik wird beim Zeichnen von Kreisen benutzt. \Circle(r) zeichnet einen Kreis mit Radius r um die aktuelle Cursorposition, \CircleAt(x,y)(r) zeichnet den Kreis um den Punkt (x,y).
MGA-TeX kann aber noch viel mehr! Die nächste Zeichnung soll ein Achsenkreuz und den Graphen der Sinusfunktion enthalten.
Für das Zeichnen der Funktion y=a·sin(bx+c) + d in den Grenzen von u bis v steht der Befehl \Sinus(a,b,c,d)(u,v)[n] zur Verfügung. Die Zahl n bestimmt, aus wie vielen Streckenstücken der Graph zusammengesetzt werden soll.
Für das Zeichnen der gewöhnlichen Sinusfunktion muss also a=1, b=1, c=0 und d=0 gesetzt werden. Will man die Funktion auf dem Intervall [-4,8] zeichnen, so umfasst das 12cm. Die Kurve wird glatt genug, wenn man sie aus 120 Streckenstücken zusammensetzt. Das passt alles in eine Zeichnung von 12×3 cm, der Nullpunkt kann an die Stelle (4,1.5) gesetzt werden.
\InitGraph{12}{3}{4}{1.5}{1cm}
\Axes
\Sinus(1,1,0,0)(-4,8)[120]
\CloseGraph
Will man die Achsen markieren und zusätzlich zur Sinusfunktion auch eine Cosinusfunktion
(also eine um pi/2 verschobene Sinusfunktion) im Koordinatensystem einzeichnen, so kann man
das folgendermaßen machen:
\InitGraph{12}{5}{4}{2}{1cm}
\StickAxes(\EinPi,2)(1,1)
\Sinus(1,1,0,0)(-4,8)[120]
\SetDashed
\Sinus(1,1,\PiHalbe,0)(-4,8)[120]
\CloseGraph
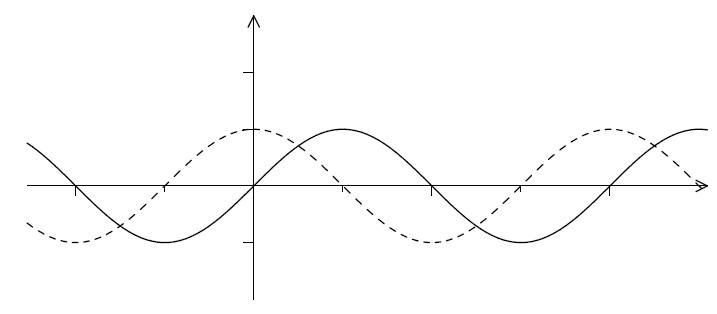
Noch besser wird das Bild, wenn man die Graphen farbig zeichnet und
die Achsen beschriftet.
\usepackage[ps,col]{mgtex_24} Die Option col ermöglicht den Gebrauch von Farben!
...
\begin{document}
...
\InitGraph{12}{5}{4}{2}{1cm}
\SetThick{0.8pt} Hier wird die Liniendicke auf 0.8pt gesetzt.
\SetCMYKColor(1,0,0,0) Ab jetzt wird in Cyan gezeichnet.
\Sinus(1,1,0,0)(-4,8)[120]
\TextAt(\PiHalbe,1)[tr]{\TextColor{$y=\sin x$}} Damit sich die Farbe auf den Text auswirkt,
muss der Befehl \TextColor{...} eingesetzt werden.
\SetCMYKColor(0,0.3,1,0) Ab jetzt wird mit einer anderen Farbe gezeichnet.
\Sinus(1,1,\PiHalbe,0)(-4,8)[120]
\TextAt(\ZweiPi,1)[t]{\TextColor{$y=\cos x$}}
\ResetColor Ab jetzt wieder in Schwarz zeichnen!
\SetNormal Liniendicke auf Standard zurücksetzen!
\UserLine[1](2,1){$\pi$}
\UserLine[3](2,1){$\pi$}
\Coordinates(\EinPi,2)(1,1)
\CloseGraph
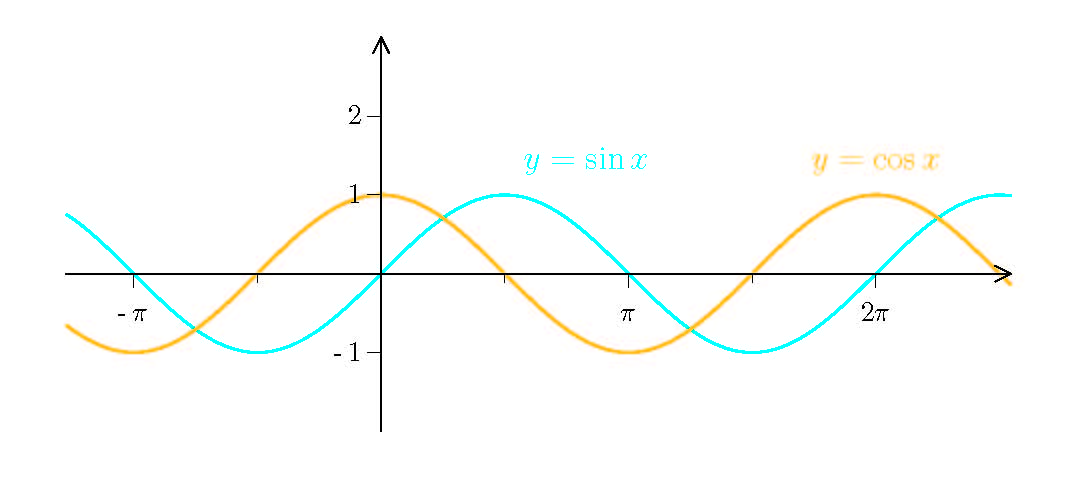
Noch ein paar Worte zu den Farb-Befehlen, zur Text- und zur Koordinaten-Darstellung:
Es gibt zwei Farbmodelle, nämlich RGB (red, green, blue), optimiert für die Bildschirmausgabe, und CMYK (cyan, magenta, yellow, black), optimiert für die Druckausgabe. Die Zahlenwerte bewegen sich zwischen 0 und 1. \SetCMYKColor(0,1,0,0) liefert den reinen Farbton Magenta, \SetCMYKColor(0,0.5,0.5,0) als Mischung von Magenta und Gelb den Farbton Orange. Mit \ResetColor schaltet man wieder auf Schwarz zurück. Analog liefert z.B. \SetRGB(0,1,0) die Farbe Grün.
Mit \TextAt(x,y)[pos]{Text} wird der angegebene Text an einer bestimmten Position relativ zum Punkt (x,y) ausgegeben. Als Position kommen r,l,t und b (für rechts, links, top=oben und bottom=unten) und Kombinationen wie z.B. tr (für rechts-oben) in Frage.
\Coordinates(a,n)(b,m) zeichnet ein Achsenkreuz in der Grenzen der Graphik. Dabei werden Markierungen (auf der x-Achse im Abstand a und auf der y-Achse im Abstand b) angebracht, mit jeweils n bzw. m Teilabschnitten. Außerdem werden die Hauptmarkierungen (also nicht die Markierungen der Teilabschnitte) mit Zahlen beschriftet. Möchte man diese Beschriftung ändern, so kann man das für jede Halbachse einzeln tun. Das geht mit dem Befehl \UserLine[n](k,l){Zusatztext}. Die Nummer n (zwischen 1 und 4) bezeichnet die betroffene Halbachse. Ab der k-ten Markierung werden Zahlen ausgegeben, und ab der l-ten Markierung wird der Zusatztext an diese Zahlen angehängt. Ein typisches Beispiel wäre die Kombination des Befehls \UserLine[1](2,1){$\pi$} mit dem Befehl \Coordinates(\EinPi,2)(1,1). Der Befehl \UserLine muss dabei unbedingt vor dem Befehl \Coordinates stehen! Der zweite Befehl zeichnet das Koordinatensystem. Die Hauptmarkierungen auf der x-Achse haben den Abstand π=3.14..., und diese Zahl kann mit \EinPi abgekürzt werden. Die Zahl 2 als Anzahl der Teilabschnitte führt dazu, dass jeweils in der Mitte der Hauptabschnitte (also bei π/2 usw.) noch eine Markierung angebracht wird. Normalerweise stände dann bei π die Zahl 1, bei 2π die Zahl 2 usw. Durch den \UserLine-Befehl erreicht man aber, dass bei π die Beschriftung 'π' (nicht '1π') steht, bei 2π die Beschriftung '2π' usw.
Nun ein noch komplexeres Beispiel:
Es gibt zwei Farbmodelle, nämlich RGB (red, green, blue), optimiert für die Bildschirmausgabe, und CMYK (cyan, magenta, yellow, black), optimiert für die Druckausgabe. Die Zahlenwerte bewegen sich zwischen 0 und 1. \SetCMYKColor(0,1,0,0) liefert den reinen Farbton Magenta, \SetCMYKColor(0,0.5,0.5,0) als Mischung von Magenta und Gelb den Farbton Orange. Mit \ResetColor schaltet man wieder auf Schwarz zurück. Analog liefert z.B. \SetRGB(0,1,0) die Farbe Grün.
Mit \TextAt(x,y)[pos]{Text} wird der angegebene Text an einer bestimmten Position relativ zum Punkt (x,y) ausgegeben. Als Position kommen r,l,t und b (für rechts, links, top=oben und bottom=unten) und Kombinationen wie z.B. tr (für rechts-oben) in Frage.
\Coordinates(a,n)(b,m) zeichnet ein Achsenkreuz in der Grenzen der Graphik. Dabei werden Markierungen (auf der x-Achse im Abstand a und auf der y-Achse im Abstand b) angebracht, mit jeweils n bzw. m Teilabschnitten. Außerdem werden die Hauptmarkierungen (also nicht die Markierungen der Teilabschnitte) mit Zahlen beschriftet. Möchte man diese Beschriftung ändern, so kann man das für jede Halbachse einzeln tun. Das geht mit dem Befehl \UserLine[n](k,l){Zusatztext}. Die Nummer n (zwischen 1 und 4) bezeichnet die betroffene Halbachse. Ab der k-ten Markierung werden Zahlen ausgegeben, und ab der l-ten Markierung wird der Zusatztext an diese Zahlen angehängt. Ein typisches Beispiel wäre die Kombination des Befehls \UserLine[1](2,1){$\pi$} mit dem Befehl \Coordinates(\EinPi,2)(1,1). Der Befehl \UserLine muss dabei unbedingt vor dem Befehl \Coordinates stehen! Der zweite Befehl zeichnet das Koordinatensystem. Die Hauptmarkierungen auf der x-Achse haben den Abstand π=3.14..., und diese Zahl kann mit \EinPi abgekürzt werden. Die Zahl 2 als Anzahl der Teilabschnitte führt dazu, dass jeweils in der Mitte der Hauptabschnitte (also bei π/2 usw.) noch eine Markierung angebracht wird. Normalerweise stände dann bei π die Zahl 1, bei 2π die Zahl 2 usw. Durch den \UserLine-Befehl erreicht man aber, dass bei π die Beschriftung 'π' (nicht '1π') steht, bei 2π die Beschriftung '2π' usw.
Nun ein noch komplexeres Beispiel:
Der TeX-Code dafür sieht folgendermaßen aus:
\InitGraph{12}{5}{4}{2}{1cm}
\SetThick{0.8pt}
\SetCMYKColor(0.2,0,0,0)
\SetColShading
\Sinus(2,0.5,0,0.5)(0.5,4.5)[40]
\ColShadingOff
\SetCMYKColor(1,0,0,0)
\Sinus(2,0.5,0,0.5)(-\EinPi,\ZweiPi)[100]
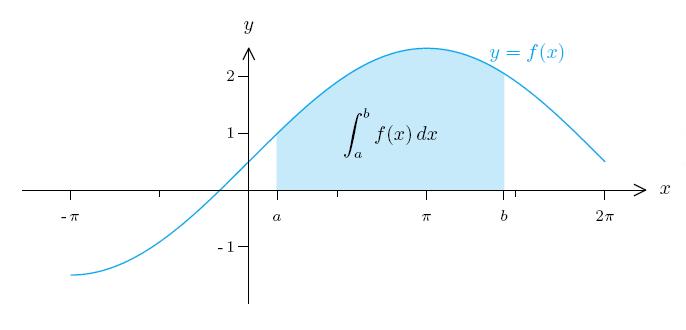
\TextAt(4,2)[tr]{\TextColor{$y=f(x)$}}
\SetCMYKColor(0,0.3,0.7,0)
\ResetColor
\SetNormal
\XLabelAt(0.5){$\mathstrut a$}
\XLabelAt(4.5){$\mathstrut b$}
\TextAt(2.5,1)[c]{$\DST \int_a^b f(x)\,dx$}
\UserLine[1](2,1){$\pi$}
\UserLine[3](2,1){$\pi$}
\BCoordinates(\EinPi,2)(1,1)<7,2.5>
\TextAt(7,0)[r]{$x$}
\TextAt(0,2.5)[t]{$y$}
\CloseGraph
Soll die Fläche unter einem Funktionsgraphen eingefärbt werden, so geht man folgendermaßen vor:
Weitere Erklärungen zu den oben verwendeten Befehlen finden Sie im Handbuch.
Bei Gelegenheit soll dieses Tutorial weitergeführt werden.
- Zunächst wird die gewünschte Farbe eingestellt: \SetCMYKColor(0.2,0,0,0)
- Der Befehl \SetColShading startet den Färbevorgang.
- Mit \Sinus(2,0.5,0,0.5)(0.5,4.5)[40] wird der Funktionsgraph von y=2 sin(0.5 x)+0.5 im Bereich zwischen 0.5 und 4.5 nicht gezeichnet, sondern es werden ca. 40 gefärbte schmale Trapeze zwischen x-Achse und Funktionsgraph eingefügt. Wählt man etwa 400 statt 40 Abschnitte, so sieht das Ganze glatter aus, kostet aber mehr Rechenzeit.
- \ColShadingOff beendet den Färbevorgang. Die Farbe muss zusätzlich abgeschaltet werden, durch \ResetColor oder einen neuen Farbbefehl.
- Will man den Funktionsgraphen auch noch als Linie sehen, so muss nun der Befehl dafür noch mal extra gegeben werden.
Weitere Erklärungen zu den oben verwendeten Befehlen finden Sie im Handbuch.
Bei Gelegenheit soll dieses Tutorial weitergeführt werden.
