- Why Numerical Result Verification?
- A Brief History of Computing
- Existing solutions for standard Algorithms
Why Numerical Result Verification?
Floating-point arithmetic is the fast way to perform scientific and engineering calculations. Today, individual floating-point operations on most computers are of maximum accuracy in the sense that the rounded result differs at most by 1 unit in the last place from the exact result. However, after two or more operations, the result can be completely wrong. Computers now carry out up to 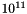 floating-point operations per second. Thus, particular attention must be paid to the reliability of the computed results. In recent years, techniques have been developed in numerical analysis which make it possible for the computer itself to verify the correctness of computed results for numerous problems and applications. Moreover, the computer frequently establishes the existence and uniqueness of the solution in this way. For example, a verified solution of a system of ordinary differential equations is just as valid as a solution obtained by a computer algebra system, which still requires a valid formula evaluation. Furthermore, the numerical routine remains applicable even if the problem does not have a closed-form solution.
floating-point operations per second. Thus, particular attention must be paid to the reliability of the computed results. In recent years, techniques have been developed in numerical analysis which make it possible for the computer itself to verify the correctness of computed results for numerous problems and applications. Moreover, the computer frequently establishes the existence and uniqueness of the solution in this way. For example, a verified solution of a system of ordinary differential equations is just as valid as a solution obtained by a computer algebra system, which still requires a valid formula evaluation. Furthermore, the numerical routine remains applicable even if the problem does not have a closed-form solution.
A Brief History of Computing
Methods of calclulation have put their stamp on mathematics throughout history. Progress in connection with numbers has meant progress in mathematics also. The invention of mechanical calculating machines by B. Pascal, G. W. Leibniz, and others, of logarithms and the slide rule, and of many other mechanical and analog computational aids, represent significant milestones in scientific computing.
A great leap in development took place about 50 years ago with the development of the first electronic computers. This technology iommediately made it possible to perform arithmetic operations faster than its mechanical or electromechanical predeccors by a factor of about 1000. The great technological gains of this century would have been impossible without modern computation. Today's automobile, airplane, space travel, modern radio and television, and not least the rapid further development of the computer itself wre enabled by enormous computational capacity. On the other hand, advances in computer hardware gave massive stimulation to further development of algorithmic and numerical mathematics.
Further development of circuit technology, which again would not have been possible without the computer, has increased the computational capacity of a processor by a factor of about 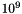 , compared to the first electronic computers of the 1950`s. Comparison of the numbers
, compared to the first electronic computers of the 1950`s. Comparison of the numbers 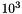 and
and 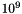 shows that the real computer revolution took place after the development of the first electronic computers. Remarkably, there was nothing equivalent to this development on the arithmetical-mathematical side. The enormous advances in computer technology really suggested an attempt to make the computer also more powerful arithmetically. On this, however, mathematicians exerted hardly any influence. In the area of scientific and engineering applications of cencern here, the computer is used today in especially the same way as it was in the middle 1950`s. The same four floating-point operations of addition, subtraction, multiplication, and division are still being performed, albeit much faster.
shows that the real computer revolution took place after the development of the first electronic computers. Remarkably, there was nothing equivalent to this development on the arithmetical-mathematical side. The enormous advances in computer technology really suggested an attempt to make the computer also more powerful arithmetically. On this, however, mathematicians exerted hardly any influence. In the area of scientific and engineering applications of cencern here, the computer is used today in especially the same way as it was in the middle 1950`s. The same four floating-point operations of addition, subtraction, multiplication, and division are still being performed, albeit much faster.
As more and more computations can be done faster and faster, larger scientific problems can be addressed, and it becomes increasingly critical to make scientific computation more trustworthy than the exclusive use of ordinary floating-point arithmetic. This development began about 25 years ago and has gained a considerable following. However, methods for validated computation have yet to achieve universal acceptance.
Existing solutions for standard Algorithms
- Evaluation of Polynomials
- Automatic Differentiation
- Nonlinear Equations in One Variable
- Global Optimization (one-dimensional)
- Evaluation of Arithmetic Expressions
- Zeros of Complex Polynomials
- (Fast) Linear Systems of Equations
- Linear Optimization
- Automatic Differentiation for Gradients, Jacobians and Hessians
- Nonlinear Systems of Equations
- Global Optimization (multi-dimensional)
