Evaluation of Polynomials
Overview
On this page, we consider the evaluation of a polynomial function of a single variable. We usually compute the value of an arithmetic function by replacing each arithmetic operation by its corresponding floating-point machine operation. Roundoff errors and cancellations sometimes cause the calculated result to be drastically wrong. For similar reasons, a naive interval evaluation of a polynomial may lead to intervals so large as to be practically useless. Roundoff and cancellation errors are especially dangerous if we are evaluating a function close to a root, as we will see when we compute verified enclosures of zeroes of polynomials.
We present an algorithm to evaluate a real polynomial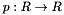 
defined as
![\[ p(t) = \sum \limits_{i=0}^n p_i t^i \;,\; p_i , t \in R \;,\; i = 0 , ... , n \;,\; p_n \not= 0 \]](form_86.png)
We assume the coefficients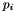 
to be representable in the floating-point number system of the host computer. The algorithm achieves maximum accuracy, even in the neighborhood of a root where cancellation dooms an ordinary floating-point evaluation.
Algorithmic Description
We present the algorithm RPolyEval for the evaluation of a real polynomial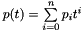 
with maximum accuracy. Except for the special cases 
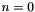and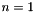 
, which can be calculated directly, an iterative solution method is used. We first compute a floating-point approximation of 
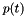. We then carry out a residual iteration by solving a linear system of equations. The new solution interval determined in the next step is checked for being of maximum accuracy, i.e. for being exact to one unit in the last place of the mantissa (1 ulp).
The RPolyEval Algorithm
Implementation and Examples
We list the C++ program code for the evaluation of a real polynomial with maximum accuracy. Interval variables are named with double characters, e.g. ![$ rr[i] $](form_92.png)
denotes the interval ![$ [r]_i $](form_93.png)
.
Module rpoly
The header file of module rpoly supplies the definition of the class RPolynomial representing a real polynomial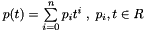 
. Since arithmetic operations for real polynomials are not required by the algorithm, they are not provided by module rpoly.
00001 /* 00002 ** CXSC is a C++ library for eXtended Scientific Computing (V 2.5.4) 00003 ** 00004 ** Copyright (C) 1990-2000 Institut fuer Angewandte Mathematik, 00005 ** Universitaet Karlsruhe, Germany 00006 ** (C) 2000-2014 Wiss. Rechnen/Softwaretechnologie 00007 ** Universitaet Wuppertal, Germany 00008 ** 00009 ** This library is free software; you can redistribute it and/or 00010 ** modify it under the terms of the GNU Library General Public 00011 ** License as published by the Free Software Foundation; either 00012 ** version 2 of the License, or (at your option) any later version. 00013 ** 00014 ** This library is distributed in the hope that it will be useful, 00015 ** but WITHOUT ANY WARRANTY; without even the implied warranty of 00016 ** MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 00017 ** Library General Public License for more details. 00018 ** 00019 ** You should have received a copy of the GNU Library General Public 00020 ** License along with this library; if not, write to the Free 00021 ** Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA 00022 */ 00023 00024 /* CVS $Id: rpoly.hpp,v 1.15 2014/01/30 17:49:27 cxsc Exp $ */ 00025 00026 //============================================================================ 00027 // 00028 // Program/Module 00029 // from 00030 // C++ TOOLBOX FOR VERIFIED COMPUTING I 00031 // Basic Numerical Problems 00032 // 00033 // Copyright (c) 1995 Rolf Hammer, Matthias Hocks, Dietmar Ratz 00034 // 00035 // For details on theory, algorithms, and programs, see the book 00036 // 00037 // R. Hammer, M. Hocks, U. Kulisch, D. Ratz: C++ Toolbox for 00038 // Verified Computing I - Basic Numerical Problems. Springer-Verlag, 00039 // Heidelberg, New York, 1995. 00040 // 00041 //============================================================================ 00042 //---------------------------------------------------------------------------- 00043 // File: rpoly (header) 00044 // Purpose: Definition of the class for the representation of a real 00045 // polynomial by its coefficients. 00046 // Class RPolynomial: 00047 // Deg() : to get the degree of the polynomial 00048 // RPolynomial(): constructors 00049 // operator [] : component access 00050 // operator >> : input operator for data of type RPolynomial 00051 // operator << : output operator for data of type RPolynomial 00052 //---------------------------------------------------------------------------- 00053 #ifndef __RPOLY_HPP 00054 #define __RPOLY_HPP 00055 00056 #include <rvector.hpp> // Real vector arithmetic 00057 00058 using namespace cxsc; 00059 using namespace std; 00060 00061 class RPolynomial { 00062 private: 00063 rvector coeff; 00064 public: 00065 RPolynomial ( int ); 00066 RPolynomial ( const RPolynomial& ); 00067 real& operator[] ( int i ) { return coeff[i]; } 00068 00069 friend int Deg ( const RPolynomial& ); 00070 friend istream& operator>> ( istream&, RPolynomial& ); 00071 friend ostream& operator<< ( ostream&, RPolynomial ); 00072 }; 00073 00074 int Deg ( const RPolynomial& ); 00075 istream& operator>> ( istream&, RPolynomial& ); 00076 ostream& operator<< ( ostream&, RPolynomial ); 00077 #endif 00078 00079 00080 00081
The input operator >> echos the indices on the standard output device to give an information on the index of the coefficient actually to be entered.
00001 /* 00002 ** CXSC is a C++ library for eXtended Scientific Computing (V 2.5.4) 00003 ** 00004 ** Copyright (C) 1990-2000 Institut fuer Angewandte Mathematik, 00005 ** Universitaet Karlsruhe, Germany 00006 ** (C) 2000-2014 Wiss. Rechnen/Softwaretechnologie 00007 ** Universitaet Wuppertal, Germany 00008 ** 00009 ** This library is free software; you can redistribute it and/or 00010 ** modify it under the terms of the GNU Library General Public 00011 ** License as published by the Free Software Foundation; either 00012 ** version 2 of the License, or (at your option) any later version. 00013 ** 00014 ** This library is distributed in the hope that it will be useful, 00015 ** but WITHOUT ANY WARRANTY; without even the implied warranty of 00016 ** MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 00017 ** Library General Public License for more details. 00018 ** 00019 ** You should have received a copy of the GNU Library General Public 00020 ** License along with this library; if not, write to the Free 00021 ** Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA 00022 */ 00023 00024 /* CVS $Id: rpoly.cpp,v 1.15 2014/01/30 17:49:27 cxsc Exp $ */ 00025 00026 //============================================================================ 00027 // 00028 // Program/Module 00029 // from 00030 // C++ TOOLBOX FOR VERIFIED COMPUTING I 00031 // Basic Numerical Problems 00032 // 00033 // Copyright (c) 1995 Rolf Hammer, Matthias Hocks, Dietmar Ratz 00034 // 00035 // For details on theory, algorithms, and programs, see the book 00036 // 00037 // R. Hammer, M. Hocks, U. Kulisch, D. Ratz: C++ Toolbox for 00038 // Verified Computing I - Basic Numerical Problems. Springer-Verlag, 00039 // Heidelberg, New York, 1995. 00040 // 00041 //============================================================================ 00042 //---------------------------------------------------------------------------- 00043 // File: rpoly (implementation) 00044 // Purpose: Definition of the class for the representation of a real 00045 // polynomial by its coefficients. 00046 // Class RPolynomial: 00047 // Deg() : to get the degree of the polynomial 00048 // RPolynomial(): constructors 00049 // operator [] : component access 00050 // operator >> : input operator for data of type RPolynomial 00051 // operator << : output operator for data of type RPolynomial 00052 //---------------------------------------------------------------------------- 00053 #include <rpoly.hpp> 00054 00055 using namespace cxsc; 00056 using namespace std; 00057 00058 int Deg ( const RPolynomial& p ) { return Ub(p.coeff); } 00059 00060 RPolynomial::RPolynomial( int n ) 00061 { 00062 Resize(coeff,0,n); 00063 coeff = 0.0; 00064 } 00065 00066 RPolynomial::RPolynomial( const RPolynomial& p ) 00067 { 00068 Resize(coeff,0,Deg(p)); 00069 coeff = p.coeff; 00070 } 00071 00072 istream& operator>> ( istream& in, RPolynomial& p ) 00073 { 00074 cout << " x^0 * "; in >> p[0]; 00075 for (int i = 1; i <= Deg(p); i++) 00076 { cout << "+ x^" << i << " * "; in >> p[i]; } 00077 return in; 00078 } 00079 00080 ostream& operator<< ( ostream& out, RPolynomial p ) 00081 { 00082 int PolyIsZero, n = Deg(p); 00083 00084 PolyIsZero = 1; 00085 for (int i = 0; i <= n; i++) { 00086 if (p[i] == 0.0) continue; 00087 if (PolyIsZero) 00088 out << " "; 00089 else 00090 out << "+ "; 00091 out << p[i] << " * x^" << i << endl; 00092 PolyIsZero = 0; 00093 } 00094 if (PolyIsZero) out << " 0 (= zero polynomial)" << endl; 00095 return out; 00096 } 00097 00098 00099 00100
Module rpeval
The header file of module rpeval supplies the interface of the function RPolyEval(), for evaluating a real polynomial with maximum accuracy and the interface of the function RPolyEvalErrMsg() which can be used to get an error message for the error code returned by RPolyEval().
00001 /* 00002 ** CXSC is a C++ library for eXtended Scientific Computing (V 2.5.4) 00003 ** 00004 ** Copyright (C) 1990-2000 Institut fuer Angewandte Mathematik, 00005 ** Universitaet Karlsruhe, Germany 00006 ** (C) 2000-2014 Wiss. Rechnen/Softwaretechnologie 00007 ** Universitaet Wuppertal, Germany 00008 ** 00009 ** This library is free software; you can redistribute it and/or 00010 ** modify it under the terms of the GNU Library General Public 00011 ** License as published by the Free Software Foundation; either 00012 ** version 2 of the License, or (at your option) any later version. 00013 ** 00014 ** This library is distributed in the hope that it will be useful, 00015 ** but WITHOUT ANY WARRANTY; without even the implied warranty of 00016 ** MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 00017 ** Library General Public License for more details. 00018 ** 00019 ** You should have received a copy of the GNU Library General Public 00020 ** License along with this library; if not, write to the Free 00021 ** Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA 00022 */ 00023 00024 /* CVS $Id: rpeval.hpp,v 1.14 2014/01/30 17:49:27 cxsc Exp $ */ 00025 00026 //============================================================================ 00027 // 00028 // Program/Module 00029 // from 00030 // C++ TOOLBOX FOR VERIFIED COMPUTING I 00031 // Basic Numerical Problems 00032 // 00033 // Copyright (c) 1995 Rolf Hammer, Matthias Hocks, Dietmar Ratz 00034 // 00035 // For details on theory, algorithms, and programs, see the book 00036 // 00037 // R. Hammer, M. Hocks, U. Kulisch, D. Ratz: C++ Toolbox for 00038 // Verified Computing I - Basic Numerical Problems. Springer-Verlag, 00039 // Heidelberg, New York, 1995. 00040 // 00041 //============================================================================ 00042 //---------------------------------------------------------------------------- 00043 // File: rpeval (header) 00044 // Purpose: Evaluation of a real polynomial p with maximum accuracy. 00045 // Global functions: 00046 // RPolyEval() : computes an enclosure for the exact value p(t) with 00047 // maximum accuracy 00048 // RPolyEvalErrMsg(): delivers an error message text 00049 //---------------------------------------------------------------------------- 00050 #ifndef __RPEVAL_HPP 00051 #define __RPEVAL_HPP 00052 00053 #include <interval.hpp> // Interval arithmetic 00054 #include <rpoly.hpp> // Real polynomial type 00055 00056 using namespace cxsc; 00057 using namespace std; 00058 00059 extern char* RPolyEvalErrMsg ( int ); 00060 extern void RPolyEval ( RPolynomial, real, real&, interval&, int&, int& ); 00061 #endif 00062 00063 00064 00065
The function RPolyEval() is an implementation of the algorithm. It computes an approximation and an enclosure of the value of the real polynomial 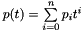with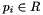 
at a point 
.
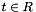00001 /* 00002 ** CXSC is a C++ library for eXtended Scientific Computing (V 2.5.4) 00003 ** 00004 ** Copyright (C) 1990-2000 Institut fuer Angewandte Mathematik, 00005 ** Universitaet Karlsruhe, Germany 00006 ** (C) 2000-2014 Wiss. Rechnen/Softwaretechnologie 00007 ** Universitaet Wuppertal, Germany 00008 ** 00009 ** This library is free software; you can redistribute it and/or 00010 ** modify it under the terms of the GNU Library General Public 00011 ** License as published by the Free Software Foundation; either 00012 ** version 2 of the License, or (at your option) any later version. 00013 ** 00014 ** This library is distributed in the hope that it will be useful, 00015 ** but WITHOUT ANY WARRANTY; without even the implied warranty of 00016 ** MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU 00017 ** Library General Public License for more details. 00018 ** 00019 ** You should have received a copy of the GNU Library General Public 00020 ** License along with this library; if not, write to the Free 00021 ** Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA 00022 */ 00023 00024 /* CVS $Id: rpeval.cpp,v 1.14 2014/01/30 17:49:27 cxsc Exp $ */ 00025 00026 //============================================================================ 00027 // 00028 // Program/Module 00029 // from 00030 // C++ TOOLBOX FOR VERIFIED COMPUTING I 00031 // Basic Numerical Problems 00032 // 00033 // Copyright (c) 1995 Rolf Hammer, Matthias Hocks, Dietmar Ratz 00034 // 00035 // For details on theory, algorithms, and programs, see the book 00036 // 00037 // R. Hammer, M. Hocks, U. Kulisch, D. Ratz: C++ Toolbox for 00038 // Verified Computing I - Basic Numerical Problems. Springer-Verlag, 00039 // Heidelberg, New York, 1995. 00040 // 00041 //============================================================================ 00042 //---------------------------------------------------------------------------- 00043 // File: rpeval (implementation) 00044 // Purpose: Evaluation of a real polynomial p with maximum accuracy. 00045 // Method: Transformation of Horner's scheme for evaluating p(t) to a linear 00046 // system of equations A(t)*x = p, where A(t) is a bidiagonal, Toeplitz 00047 // matrix and x = (x_n,...,x_0). By iterative refinement the floating- 00048 // point approximation is improved and the exact solution x is enclosed in 00049 // an interval vector [x]. 00050 // Global functions: 00051 // RPolyEval() : computes an enclosure for the exact value p(t) with 00052 // maximum accuracy 00053 // RPolyEvalErrMsg(): delivers an error message text 00054 //---------------------------------------------------------------------------- 00055 #include <string.h> // String handling 00056 #include <imatrix.hpp> // Interval matrix/vector arithmetic 00057 #include <mvi_util.hpp> // Interval matrix/vector utility functions 00058 #include <rpeval.hpp> 00059 00060 using namespace cxsc; 00061 using namespace std; 00062 00063 const int kmax = 10; // Maximum number of iteration steps 00064 00065 //--------------------------------------------------------------------------- 00066 // Error codes used in this module. In the comments below p[0],..., p[n] are 00067 // the coefficients of a polynomial p. 00068 //--------------------------------------------------------------------------- 00069 const int 00070 NoError = 0, // No error occurred 00071 ItFailed = 1; // Maximum number of iterations exceeded 00072 00073 //---------------------------------------------------------------------------- 00074 // Error messages depending on the error code. 00075 //---------------------------------------------------------------------------- 00076 char* RPolyEvalErrMsg ( int Err ) 00077 { 00078 static char Msg[80] = ""; 00079 00080 if (Err != NoError) { 00081 char Hlp[60]; 00082 00083 if (Err == ItFailed) 00084 sprintf(Hlp,"Maximum number of iterations (=%d) exceeded",kmax); 00085 else 00086 strcpy(Hlp,"Code not defined"); 00087 sprintf(Msg,"Error: %s!",Hlp); 00088 } 00089 return(Msg); 00090 } 00091 00092 //---------------------------------------------------------------------------- 00093 // Purpose: Determination of p(t) (a polynomial p with argument t) with 00094 // maximum accuracy. 00095 // Parameters: 00096 // In : 'p' : represents a real polynomial by its coefficients 00097 // 't' : specifies the point of evaluation 00098 // Out: 'z' : floating-point approximation computed by Horner's scheme 00099 // 'zz' : enclosure of p(t) 00100 // 'k' : number of iterations needed 00101 // 'Err': error flag 00102 // Description: The polynomial 'p' is defined by its coefficients and, 't' 00103 // denotes the evaluation point. Horner's scheme for evaluating p is equi- 00104 // valent to computing the solution of a linear system of equations 00105 // A(t)*x = p, where A(t) is a bidiagonal, Toeplitz matrix and 00106 // x =(x_n,...,x_0). The component x_0 of x is equal to p(t). The solution 00107 // x is enclosed in an interval vector [x] by iterative refinement. The 00108 // first element of [x] is an enclosure of p(t). It is returned in the 00109 // variable 'zz'. A floating-point approximation computed by Horner's 00110 // scheme is returned in 'z'. The number of iterations is returned in 'k' 00111 // and the state of success is returned in 'Err'. 00112 // Remark: The polynomial's coefficients and the argument are assumed to be 00113 // exact floating-point numbers! 00114 //---------------------------------------------------------------------------- 00115 void RPolyEval ( RPolynomial p, real t, real& z, 00116 interval& zz, int& k, int& Err ) 00117 { 00118 int i, j, n = Deg(p); // The j-th column of the matrix 00119 ivector rr(0,n), yy(0,n); // 'y' is used to store the j-th 00120 rvector x(0,n); // correction for the solution of 00121 rmatrix y(0,n,0,kmax); // A(t)*y = p. 00122 dotprecision Accu; //------------------------------- 00123 idotprecision IAccu; 00124 00125 k = 0; // Initialization 00126 Err = NoError; //--------------- 00127 00128 if (n == 0) // Constant polynomial 00129 { z = p[0]; zz = p[0]; } //-------------------- 00130 00131 else if (n == 1) { // Linear polynomial 00132 Accu = p[0]; //------------------ 00133 accumulate(Accu,t,p[1]); 00134 rnd(Accu,z); 00135 rnd(Accu,zz); 00136 } 00137 else { // n > 1 00138 x = 0.0; y = 0.0; // Initialization x = 0 and y = 0 00139 //-------------------------------- 00140 00141 x[n] = p[n]; // Computation of a first approxi- 00142 for (i = n-1; i >= 0; i--) // mation using Horner's scheme 00143 x[i] = x[i+1]*t + p[i]; //-------------------------------- 00144 z = x[0]; 00145 00146 y[Col(0)] = x; // Iterative refinement for the 00147 do { // solution of A*x = p 00148 //-------------------------------- 00149 if (k > 0) // If a residual was computed, its middle 00150 y[Col(k)] = mid(yy); // is stored as the next correction of 'y' 00151 00152 yy[n] = 0.0; // Computation of the residual [r] 00153 for (i = n-1; i >= 0; i--) { // and evaluation of the interval 00154 Accu = p[i]; // system A*[y] = [r] 00155 for(j = 0; j <= k; j++) Accu -= y[i][j]; 00156 for(j = 0; j <= k; j++) accumulate(Accu,t,y[i+1][j]); 00157 rnd(Accu,rr[i]); 00158 yy[i] = yy[i+1]*t + rr[i]; 00159 } 00160 00161 IAccu = yy[0]; // Determination of a new 00162 for (j = 0; j <= k; j++) IAccu += y[0][j]; // enclosure [z] of p(t) 00163 rnd(IAccu,zz); 00164 00165 k++; 00166 } while ( !(UlpAcc(zz,1) || (k > kmax)) ); 00167 00168 if ( !UlpAcc(zz,1) ) Err = ItFailed; 00169 } 00170 } 00171 00172 00173 00174
Examples
We consider the polynomial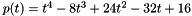 
to be evaluated in the neighborhood of the real value 
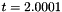and the polynomial 
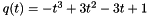to be evaluated in the neighborhood of the real value 
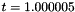. To make sure that the arguments are representable on the computer, we use the machine numbers 
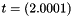and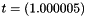 
, respectively.
Polynomial p(t) in interval [1.9995 , 2.0005]
Polynomial q(t) in interval [0.99999 , 1.00001]
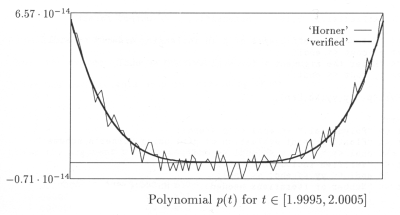
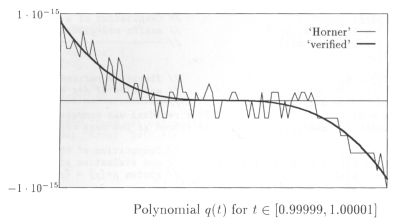
To illustrate the difficulties that may occur with the calculation of a polynomial value when using floating-point arithmetic, these two polynomials have been evaluated in floating-point arithmetic for 100 values in the neighborhood of their roots. The corresponding plots are given in the above two figures. These two examples are solved reliably using the following sample program to call RPolyEval().
00001 //============================================================================ 00002 // 00003 // Program/Module 00004 // from 00005 // C++ TOOLBOX FOR VERIFIED COMPUTING I 00006 // Basic Numerical Problems 00007 // 00008 // Copyright (c) 1995 Rolf Hammer, Matthias Hocks, Dietmar Ratz 00009 // 00010 // For details on theory, algorithms, and programs, see the book 00011 // 00012 // R. Hammer, M. Hocks, U. Kulisch, D. Ratz: C++ Toolbox for 00013 // Verified Computing I - Basic Numerical Problems. Springer-Verlag, 00014 // Heidelberg, New York, 1995. 00015 // 00016 //============================================================================ 00017 //---------------------------------------------------------------------------- 00018 // Example: Evaluation of a real polynomial with maximum accuracy 00019 //---------------------------------------------------------------------------- 00020 #include <rpeval.hpp> // Polynomial evaluation 00021 00022 00023 using namespace cxsc; 00024 using namespace std; 00025 00026 00027 int main ( ) 00028 { 00029 int Err, No, n; 00030 real t, y; 00031 interval yy; 00032 00033 do { 00034 cout << "Enter the degree of the polynomial (>=0): "; 00035 cin >> n; cout << endl; 00036 } while (n < 0); 00037 00038 RPolynomial p(n); 00039 00040 cout << SetPrecision(23,15) << Scientific; // Output format 00041 00042 cout << "Enter the coefficients of p in increasing order:" << endl; 00043 cin >> p; cout << endl; 00044 cout << "Enter the argument t for evaluation:" << endl; 00045 cin >> t; cout << endl; 00046 00047 RPolyEval(p,t,y,yy,No,Err); 00048 00049 if (!Err) { 00050 cout << "Polynomial:" << endl << p <<endl; 00051 cout << "Floating-point evaluation of p(t) using Horner's scheme:" 00052 << endl << " " << y << endl << endl; 00053 cout << "Verified inclusion of p(t):" 00054 << endl << yy << endl << endl; 00055 cout << "Number of iterations needed: " << No << endl; 00056 } 00057 else 00058 cout << RPolyEvalErrMsg(Err) << endl; 00059 00060 return 0; 00061 }
Our implementation of the algorithm produces the output listed below. In both cases the floating-point approximation, naively using Horner's nested multiplication form, does not lie within the verified enclosure of 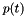and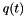 
. An even worse side effect of rounding errors occuring during the evaluation using Horner's scheme is that the standard algorithm returns not only wrong digits but also an incorrect sign for the values of 
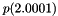and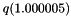 
. To avoid an incorrect interpretation of the resulting interval, we stress that this interval is numerically proved to be an enclosure of the exact value of the given polynomials for the machine numbers 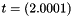and .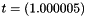
