A sparse real matrix. More...
#include <srmatrix.hpp>
Public Member Functions | |
| std::vector< int > & | column_pointers () |
Returns a reference to the vector containing the column pointers (the 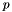 array) array) | |
| const std::vector< int > & | column_pointers () const |
Returns a constant reference to the vector containing the column pointers (the 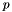 array) array) | |
| real | density () const |
| Returns the density (the number of non-zeros divided by the number of elements) of the matrix. | |
| void | dropzeros () |
| Drops explicitly stored zeros from the data structure. | |
| real & | element (int i, int j) |
| Returns a reference to the element (i,j) of the matrix. | |
| void | full (rmatrix &A) const |
| Creates a full matrix out of the sparse matrix and stores it in A. This should normally be done using the respective constructor of the dense matrix. | |
| int | get_nnz () const |
| Returns the number of non-zero entries (including explicitly stored zeros). | |
| const real | operator() (int i, int j) const |
| Returns a copy of the element in row i and column j. | |
| srmatrix_slice | operator() (const int, const int, const int, const int) |
| Returns a slice of the matrix. | |
| const srmatrix_slice | operator() (const int, const int, const int, const int) const |
| Returns a slice of the matrix. | |
| srmatrix | operator() (const intvector &pervec, const intvector &q) |
| Performs a row and column permutation using two permutation vectors. | |
| srmatrix | operator() (const intvector &pervec) |
| Performs a row permutation using a permutation vector. | |
| srmatrix | operator() (const intmatrix &P, const intmatrix &Q) |
| Performs row and column permutations using the two permutation matrices P and Q. Faster than explicitly computing the product. | |
| srmatrix | operator() (const intmatrix &P) |
| Performs a row permutation using the permutation matrix P. Faster than explicitly computing the product. | |
| srmatrix & | operator*= (const rmatrix &B) |
| Multiply the sparse matrix by B and assign the result to it. | |
| srmatrix & | operator*= (const rmatrix_slice &B) |
| Multiply the sparse matrix by B and assign the result to it. | |
| srmatrix & | operator*= (const srmatrix &B) |
| Multiply the sparse matrix by B and assign the result to it. | |
| srmatrix & | operator*= (const real &r) |
| Multiply all elements of the sparse matrix by r and assign the result to it. | |
| srmatrix & | operator+= (const rmatrix &B) |
| Add B to the sparse matrix and assign the result to it. | |
| srmatrix & | operator+= (const rmatrix_slice &B) |
| Add B to the sparse matrix and assign the result to it. | |
| srmatrix & | operator+= (const srmatrix &B) |
| Add B to the sparse matrix and assign the result to it. | |
| srmatrix & | operator-= (const rmatrix &B) |
| Subtract B from the sparse matrix and assign the result to it. | |
| srmatrix & | operator-= (const rmatrix_slice &B) |
| Subtract B from the sparse matrix and assign the result to it. | |
| srmatrix & | operator-= (const srmatrix &B) |
| Subtract B from the sparse matrix and assign the result to it. | |
| srmatrix & | operator/= (const real &r) |
| Divide all elements of the sparse matrix by r and assign the result to it. | |
| srmatrix & | operator= (const real &A) |
| Assigns a real value to all elements of the matrix (resulting in a dense matrix!) | |
| srmatrix & | operator= (const rmatrix &A) |
| Assigns a dense matrix to the sparse matrix. Only the non zero entries of the dense matrix are used. | |
| srmatrix & | operator= (const rmatrix_slice &A) |
| Assigns a dense matrix slice to the sparse matrix. Only the non zero entries of the dense matrix slice are used. | |
| srmatrix & | operator= (const srmatrix_slice &) |
| Assign a sparse matrix slice to a sparse matrix. | |
| srmatrix_subv | operator[] (const cxscmatrix_column &) |
| Returns a column of the matrix as a sparse subvector object. | |
| srmatrix_subv | operator[] (const int) |
| Returns a row of the matrix as a sparse subvector object. | |
| const srmatrix_subv | operator[] (const cxscmatrix_column &) const |
| Returns a column of the matrix as a sparse subvector object. | |
| const srmatrix_subv | operator[] (const int) const |
| Returns a row of the matrix as a sparse subvector object. | |
| std::vector< int > & | row_indices () |
Returns a reference to the vector containing the row indices (the 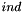 array) array) | |
| const std::vector< int > & | row_indices () const |
Returns a constant reference to the vector containing the row indices (the 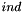 array) array) | |
| srmatrix () | |
| Standard constructor, creates an empty matrix of dimension 0x0. | |
| srmatrix (const int r, const int c) | |
| Creates an empty matrix with r rows and c columns, pre-reserving space for 2*(r+c) elements. | |
| srmatrix (const int r, const int c, const int e) | |
| Creates an empty matrix with r rows and c columns, pre-reserving space for e elements. | |
| srmatrix (const int m, const int n, const int nnz, const intvector &rows, const intvector &cols, const rvector &values, const enum STORAGE_TYPE t=triplet) | |
| Creates a sparse matrix out of three vectors (arrays) forming a matrix stored in triplet, compressed row or compressed column storage. | |
| srmatrix (const int m, const int n, const int nnz, const int *rows, const int *cols, const real *values, const enum STORAGE_TYPE t=triplet) | |
| Creates a sparse matrix out of three arrays forming a matrix stored in triplet, compressed row or compressed column storage. | |
| srmatrix (const rmatrix &A) | |
| Creates a sparse matrix out of a dense matrix A. Only the non zero elements of A are stored explicitly. | |
| srmatrix (const int ms, const int ns, const rmatrix &A) | |
| Constructor for banded matrices. | |
| srmatrix (const srmatrix_slice &) | |
| Creates a sparse matrix out of a sparse matrix slice. | |
| std::vector< real > & | values () |
Returns a reference to the vector containing the stored values (the 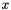 array) array) | |
| const std::vector< real > & | values () const |
Returns a constant reference to the vector containing the stored values (the 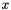 array) array) | |
Friends | |
| srmatrix | abs (const srmatrix &) |
| Returns the componentwise absolute value of A. | |
| srmatrix | abs (const scmatrix &) |
| Returns the componentwise absolute value of the sparse matrix A. | |
| srmatrix | absmax (const simatrix &) |
| Returns the componentwise maximum absolute value. | |
| srmatrix | absmin (const simatrix &) |
| Returns the componentwise minimum absolute value. | |
| int | ColLen (const srmatrix &) |
| Returns the number of rows of the matrix. | |
| srmatrix | CompMat (const simatrix &) |
| Returns Ostroswkis comparison matrix for A. | |
| srmatrix | CompMat (const srmatrix &) |
| Returns Ostrowskis comparison matrix for A. | |
| srmatrix | CompMat (const scmatrix &) |
| Returns Ostrowskis comparison matrix for A. | |
| srmatrix | CompMat (const scimatrix &) |
| Returns Ostroswkis comparison matrix for A. | |
| srmatrix | diam (const simatrix &) |
| Returns the componentwise diameter of A. | |
| srmatrix | Id (const srmatrix &) |
| Return a sparse unity matrix of the same dimension as A. | |
| srmatrix | Im (const scmatrix &) |
| Returns the imaginary part of the sparse matrix A. | |
| srmatrix | Inf (const simatrix &) |
| Returns the Infimum of the matrix A. | |
| srmatrix | InfIm (const scimatrix &) |
| Returns the imaginary part of the infimum of the matrix A. | |
| srmatrix | InfRe (const scimatrix &) |
| Returns the real part of the infimum of the matrix A. | |
| int | Lb (const srmatrix &, int) |
| Returns the lower index bound for the rows or columns of A. | |
| srmatrix | mid (const simatrix &) |
| Returns the midpoint matrix for A. | |
| std::istream & | operator>> (std::istream &, srmatrix_slice &) |
| Standard input operator for sparse matrix slice. | |
| std::istream & | operator>> (std::istream &, srmatrix_subv &) |
| Standard input operator for subvectors. | |
| srmatrix | Re (const scmatrix &) |
| Returns the real part of the sparse matrix A. | |
| int | RowLen (const srmatrix &) |
| Returns the number of columns of the matrix. | |
| void | SetLb (srmatrix &, const int, const int) |
| Sets the lower index bound of the rows (i==ROW) or columns (i==COL) to j. | |
| void | SetUb (srmatrix &, const int, const int) |
| Sets the upper index bound of the rows (i==ROW) or columns (i==COL) to j. | |
| srmatrix | Sup (const simatrix &) |
| Returns the Supremum of the matrix A. | |
| srmatrix | SupIm (const scimatrix &) |
| Returns the imaginary part of the supremum of the matrix A. | |
| srmatrix | SupRe (const scimatrix &) |
| Returns the real part of the supremum of the matrix A. | |
| srmatrix | transp (const srmatrix &) |
| Returns the transpose of A. | |
| int | Ub (const srmatrix &, int) |
| Returns the upper index bound for the rows or columns of A. | |
Detailed Description
A sparse real matrix.
Sparse matrices in C-XSC are stored in the Compressed Column Storage (CCS) format. The non zero entries of the matrix are stored in three arrays (STL-vectors) 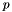 ,
, 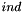 ,
, 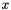 . The array
. The array 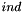 stores the row indices of the non zero elements, the array
stores the row indices of the non zero elements, the array 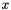 the respective values (the
the respective values (the 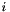 -th element of
-th element of 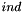 corresponds to the i-th element of
corresponds to the i-th element of 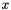 ,
, 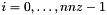 , where
, where 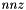 is the number of non zeros. The entries are sorted by column. The array
is the number of non zeros. The entries are sorted by column. The array 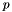 of size
of size 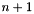 stores the starting indices for the entries of each column of the matrix, so that the entries of the
stores the starting indices for the entries of each column of the matrix, so that the entries of the 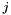 -th column of the matrix are stored in the elements with index
-th column of the matrix are stored in the elements with index ![$ p[j] $](form_377.png) through
through ![$ p[j+1]-1 $](form_378.png) of the arrays
of the arrays 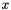 and
and 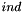 . The elements of each column are stored as sorted by the row indices, explicitly stored zeros are allowed.
. The elements of each column are stored as sorted by the row indices, explicitly stored zeros are allowed.
The internal data structure uses 0-based indexing throughout. However, in the interface to the user (using the respective operators) every matrix possesses a lower and an upper row index bound 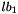 ,
, 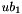 and a lower and an upper column index bound
and a lower and an upper column index bound 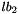 ,
, 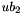 of type int. By default, these indexes are 1-based.
of type int. By default, these indexes are 1-based.
It is possible to directly access the internal data structure through the appropriate member function to allow for easier interfacing with other sparse matrix libraries and writing of more efficient sparse matrix algorithms. In this case, the user has to take care that the data structure remains consistent with the format described above. If the user just works with the operators and functions provided by C-XSC, everything will be handled automatically by the C-XSC library.
All matrix and vector operators which require dot product computations use higher precision dot products provided by the dotprecision classes. The precision to be used for these implicit dot products can be choosen by setting the global variable opdotprec accordingly. A value of 0 means maximum accuracy (the default, always used by all older C-XSC versions), a value of 1 means double accuracy, a value of 2 or higher means k-fold double accuracy. Lower accuracy leads to (significantly) faster computing times, but also to less exact results. For all dot products with an interval result, error bounds are computed to guarantee a correct enclosure. For all other dot products approximations without error bounds are computed.
- See also:
- cxsc::dotprecision
Definition at line 77 of file srmatrix.hpp.
Constructor & Destructor Documentation
| cxsc::srmatrix::srmatrix | ( | const int | m, |
| const int | n, | ||
| const int | nnz, | ||
| const intvector & | rows, | ||
| const intvector & | cols, | ||
| const rvector & | values, | ||
| const enum STORAGE_TYPE | t = triplet |
||
| ) | [inline] |
Creates a sparse matrix out of three vectors (arrays) forming a matrix stored in triplet, compressed row or compressed column storage.
Creates a sparse matrix of dimension 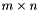 with the values from the three arrays rows, cols and values. These are interpreted according to the storage type t. For triplet rows and cols contains the indices of all non zero values and the array values contains the actual values. For compressed_column, the arrays are interpreted according to the compressed column storage format, where cols contains the column pointers. For compressed_row the arrays are interpreted according to the compressed row storage format, which is equivalent to compressed column storage with the role of the rows and columns interchanged.
with the values from the three arrays rows, cols and values. These are interpreted according to the storage type t. For triplet rows and cols contains the indices of all non zero values and the array values contains the actual values. For compressed_column, the arrays are interpreted according to the compressed column storage format, where cols contains the column pointers. For compressed_row the arrays are interpreted according to the compressed row storage format, which is equivalent to compressed column storage with the role of the rows and columns interchanged.
In each case the arrays need not be sorted by rows or columns and may contain explicit zero entries.
Definition at line 151 of file srmatrix.hpp.
| cxsc::srmatrix::srmatrix | ( | const int | m, |
| const int | n, | ||
| const int | nnz, | ||
| const int * | rows, | ||
| const int * | cols, | ||
| const real * | values, | ||
| const enum STORAGE_TYPE | t = triplet |
||
| ) | [inline] |
Creates a sparse matrix out of three arrays forming a matrix stored in triplet, compressed row or compressed column storage.
Creates a sparse matrix of dimension 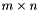 with the values from the three arrays rows, cols and values. These are interpreted according to the storage type t. For triplet rows and cols contains the indices of all non zero values and the array values contains the actual values. For compressed_column, the arrays are interpreted according to the compressed column storage format, where cols contains the column pointers. For compressed_row the arrays are interpreted according to the compressed row storage format, which is equivalent to compressed column storage with the role of the rows and columns interchanged.
with the values from the three arrays rows, cols and values. These are interpreted according to the storage type t. For triplet rows and cols contains the indices of all non zero values and the array values contains the actual values. For compressed_column, the arrays are interpreted according to the compressed column storage format, where cols contains the column pointers. For compressed_row the arrays are interpreted according to the compressed row storage format, which is equivalent to compressed column storage with the role of the rows and columns interchanged.
In each case the arrays need not be sorted by rows or columns and may contain explicit zero entries.
Definition at line 263 of file srmatrix.hpp.
| cxsc::srmatrix::srmatrix | ( | const int | ms, |
| const int | ns, | ||
| const rmatrix & | A | ||
| ) | [inline] |
Constructor for banded matrices.
Creates a sparse banded matrix of dimension 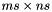 , whose bands are defined by the columns of the dense matrix A. The column inde range of A must be set appropriately: The columns of with negative indices are used for bands below the diagonal, the column with index 0 is used for the diagonal, and columns with positive index are use for bands above the diagonal.
, whose bands are defined by the columns of the dense matrix A. The column inde range of A must be set appropriately: The columns of with negative indices are used for bands below the diagonal, the column with index 0 is used for the diagonal, and columns with positive index are use for bands above the diagonal.
Definition at line 394 of file srmatrix.hpp.
Member Function Documentation
| void cxsc::srmatrix::dropzeros | ( | ) | [inline] |
Drops explicitly stored zeros from the data structure.
Dropping explicit zero entries can be essential when interfacing with other sparse matrix libraries. Some librares using the CCS storage format do not allow explicitly stored zeros.
Definition at line 449 of file srmatrix.hpp.
| real& cxsc::srmatrix::element | ( | int | i, |
| int | j | ||
| ) | [inline] |
Returns a reference to the element (i,j) of the matrix.
This function should only be used for write access. The indices i and j must be used according to the current index range of the matrix. A reference to the element (i,j) is returned. If the element is not stored explicitly, it is created as an explicit 0 entry. For read access to a single element, the ()-opeator should be used.
This function is faster than using the []-operator (for example A[i][j]), since it does not need to create a temporary subvector first.
Note that due to the underlying data structure the access to single elements of a sparse matrix is much more expensive than to the elements of a dense matrix.
Definition at line 525 of file srmatrix.hpp.
Referenced by cxsc::srmatrix_slice::element().
| const real cxsc::srmatrix::operator() | ( | int | i, |
| int | j | ||
| ) | const [inline] |
Returns a copy of the element in row i and column j.
This operator can be used for read access only. The indices i and j must be used according to the current index range of the matrix. A copy of the element (i,j) is returned, or 0 if this element is not explicitly stored. For write access to a single element, the []-opeator or the member function element should be used.
Note that due to the underlying data structure the access to single elements of a sparse matrix is much more expensive than to the elements of a dense matrix.
Definition at line 504 of file srmatrix.hpp.
Friends And Related Function Documentation
| int Lb | ( | const srmatrix & | A, |
| int | i | ||
| ) | [friend] |
Returns the lower index bound for the rows or columns of A.
If i==ROW, the lower index bound for the rows is returned, if i==COL, the lower index bound for the columns is returned.
Definition at line 881 of file srmatrix.hpp.
Referenced by operator()(), and srmatrix().
| std::istream& operator>> | ( | std::istream & | is, |
| srmatrix_slice & | M | ||
| ) | [friend] |
Standard input operator for sparse matrix slice.
The input format is set by global flags, default is dense input. Use cout << SparseInOut; for sparse input or cout << MatrixMarketInOut; for input in matrix market format.
Definition at line 2143 of file srmatrix.hpp.
| void SetLb | ( | srmatrix & | A, |
| const int | i, | ||
| const int | j | ||
| ) | [friend] |
Sets the lower index bound of the rows (i==ROW) or columns (i==COL) to j.
If i==ROW, the lower index bound for the rows of A ist set to j. if i==COL, the lower index bound of the columns is set to j. The upper index bound is automatically set according to the number of rows or columns of the matrix.
Definition at line 852 of file srmatrix.hpp.
| void SetUb | ( | srmatrix & | A, |
| const int | i, | ||
| const int | j | ||
| ) | [friend] |
Sets the upper index bound of the rows (i==ROW) or columns (i==COL) to j.
If i==ROW, the upper index bound for the rows of A ist set to j. if i==COL, the upper index bound of the columns is set to j. The lower index bound is automatically set according to the number of rows or columns of the matrix.
Definition at line 867 of file srmatrix.hpp.
| int Ub | ( | const srmatrix & | A, |
| int | i | ||
| ) | [friend] |
Returns the upper index bound for the rows or columns of A.
If i==COL, the upper index bound for the rows is returned, if i==COL, the upper index bound for the columns is returned.
Definition at line 894 of file srmatrix.hpp.
Referenced by srmatrix().
The documentation for this class was generated from the following files:
