Verified Numerics meets Computer Algebra

intpakX combines Interval Arithmetic with the features of a Computer Algebra System. It offers a variety of algorithms for the use with Maple(TM). Thus, you can do verified computations and at the same time get your results graphically visualized.

View a list of the most important functions and operators
intpakX offers.
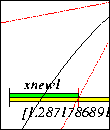
The Interval version of the Newton Method lets you find all zeros of a
continuously differentiable function and moreover gives you a proof for
the existence of unique zeros.
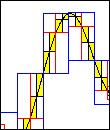
You can enclose the range of a real-valued function in one real variable
using either equidistant or adaptive subdivision and either interval
evaluation or the mean value form.
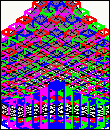
As well as for functions in one real variable, you can also compute
range enclosures for real-valued functions in two variables and
visualize the resulting intervals.
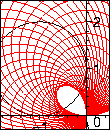
Make use of complex disc arithmetic types and operations to enclose the
range of a complex polynomial or compute the exponential function for
disc intervals.
Download intpakX or one of the available preprints or get in
contact with us.