Example: Interval Newton Method

Find enclosing intervals for all zeros of f on the interval [1.05,1.5].
Let
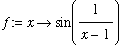 .
.
Here's the Maple Worksheet solving the task with intpakX.
Doing 10 iteration steps, you can prove the
existence of two zeros and find two intervals which must contain
every further zero of the function on the interval. Further iteration
steps and a smaller parameter for the accuracy would yield more detailed
results.
> restart;
> libname:="/usr/maple/intpakX/lib", libname;
>
with(intpakX);
And this is the solution:
> f:=x->sin(1/(x-1));
![]()
> X:=[1.05,1.5];
![]()
> compute_all_zeros_with_plot(f,X,0.001);
Enter maximal number of iteration steps: 10;
Digits = 10
Iteration step 1
xold= [1.05, 1.5]
xnew1= [1.276187073, 1.5]
xnew2= [1.05, 1.273812927]
![[Maple Plot]](images_newton1/newton_sin1dx_o16.gif)
Iteration step 2
xold= [1.276187073, 1.5]
xnew1= [1.276187073, 1.347259211]
![[Maple Plot]](images_newton1/newton_sin1dx_o17.gif)
Iteration step 3
xold= [1.276187073, 1.347259211]
xnew1= [1.316783008, 1.320737304]
![[Maple Plot]](images_newton1/newton_sin1dx_o18.gif)
Iteration step 4
xold= [1.316783008, 1.320737304]
xnew1= [1.318303507, 1.318314830]
![[Maple Plot]](images_newton1/newton_sin1dx_o19.gif)
Iteration step 5
xold= [1.05, 1.273812927]
xnew1= [1.162172903, 1.273812927]
xnew2= [1.05, 1.161640024]
![[Maple Plot]](images_newton1/newton_sin1dx_o20.gif)
Iteration step 6
xold= [1.05, 1.161640024]
xnew1= [1.105883079, 1.161640024]
xnew2= [1.05, 1.105756945]
![[Maple Plot]](images_newton1/newton_sin1dx_o21.gif)
Iteration step 7
xold= [1.105883079, 1.161640024]
xnew1= [1.144181348, 1.161640024]
xnew2= [1.105883079, 1.123341755]
![[Maple Plot]](images_newton1/newton_sin1dx_o22.gif)
Iteration step 8
xold= [1.144181348, 1.161640024]
xnew1= [1.158186203, 1.161255603]
![[Maple Plot]](images_newton1/newton_sin1dx_o23.gif)
Iteration step 9
xold= [1.158186203, 1.161255603]
xnew1= [1.159140063, 1.159163842]
![[Maple Plot]](images_newton1/newton_sin1dx_o24.gif)
Iteration step 10
xold= [1.105883079, 1.123341755]
xnew1= [1.105883079, 1.107392352]
![[Maple Plot]](images_newton1/newton_sin1dx_o25.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Number of enclosures of zeros: 4
Number of iteration steps: 10
>