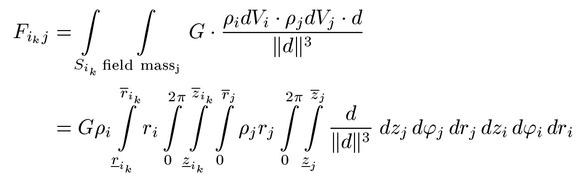Project "Newton's constant of gravitation and
verified numerical quadrature"
Researchers
Oliver Holzmann
Bruno Lang
Duration and funding
about 1995 to 2000
Description
Newton's constant of gravitation, G, is one of the fundamental
quantities in physics. While other constants, such as the speed of light,
are known to at least eight significant digits, the precision of
G is much lower. In fact, even the claim of knowing this constant
to four decimals is dubious, since different experiments lead
to values of G differing in the third digit, implying
that some of the published values must contain unknown errors.
It is therefore essential to address all sources of errors in the process
of obtaining a value for G from a physical experiment.
In an experiment carried out at the University of Wuppertal, two pendulums
are positioned between two heavy "field masses." Since the
gravitational force on a pendulum depends on its distance to the field
masses, moving the latter with spindles also increases or decreases the
distance of the pendulums from each other.
The constant G can be determined from this movement of the
pendulums relative to each other. This process involves computing
sixtuple integrals of the form
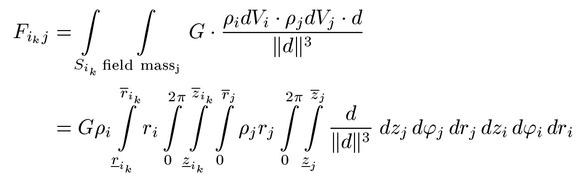
where the integration is over the volumina of one field mass and (a part of)
one pendulum with densities ρ, and d denotes the directed
distance between the respective points. Due to the complicated geometry of
the pendulums they are subdivided into segments S( i, k ).
In this project we have developed adaptive techniques that yield the
value of a multi-dimensional integral with a guaranteed
prescribed maximum error.
Using these methods we were able to show that
- the numerical evaluation of the integrals is no obstacle to the
desired goal, which is to determine G to at least four,
or even five, decimals,
- most of the geometric tolerances in the experiment are also
harmless, but
- some of the current tolerances must be reduced significantly in
order to achieve the desired accuracy. In particular, the
temperature must be monitored very carefully because it has a
major influence on the position of the field masses.
Project-related publications
|
[1]
|
Bruno Lang.
Derivative-based subdivision in multi-dimensional verified Gaussian
quadrature.
In Götz Alefeld, Jiři Rohn, Siegfried Rump, and Tetsuro
Yamamoto, editors, Symbolic Algebraic Methods and Verification Methods,
pages 145--152, Wien, 2001. Springer-Verlag.
[ DOI |
Abstract ]
|
|
[2]
|
Bruno Lang.
A comparison of subdivision strategies for verified multi-dimensional
Gaussian quadrature.
In Tibor Csendes, editor, Developments in Reliable Computing ---
SCAN-98 Proceedings, pages 67--75, Dordrecht, The Netherlands, 1999. Kluwer
Academic Publishers.
[ DOI |
Abstract ]
|
|
[3]
|
Bruno Lang.
Verified quadrature in determining Newton's constant of
gravitation.
J. Univers. Comput. Sci., 4(1):16--24, 1998.
[ DOI |
Abstract ]
|
|
[4]
|
Oliver Holzmann, Bruno Lang, and Holger Schütt.
Newton's constant of gravitation and verified numerical quadrature.
Reliab. Comput., 2(3):229--239, November 1996.
[ DOI |
Abstract ]
|
See also
the other projects involving result-verifying techniques on the
Research page