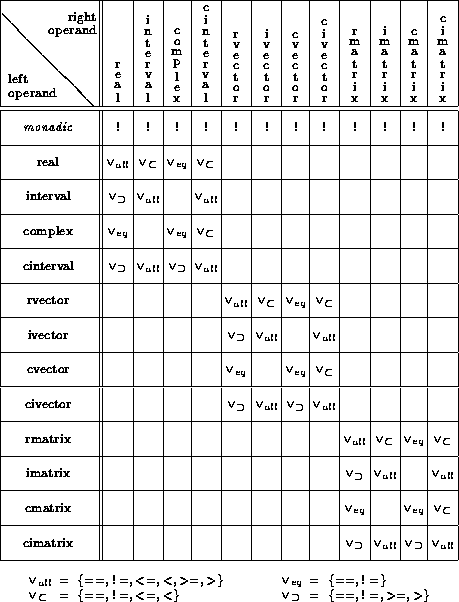
Table 3: Predefined Relational Operators
C-XSC provides a special notation to manipulate subarrays of
vectors and matrices. Subarrays are arbitrary rectangular parts of
arrays.
All predefined operators may also use subarrays as operands.
A subarray of a matrix or vector is accessed using
the ()-operator or the []-operator.
The ()-operator specifies a
subarray of an object of the same type as the original object.
For example, if A is a real nxn-matrix,
then A(i,i) is the left upper ixi submatrix.
Note that parentheses in the declaration of a dynamic vector or
matrix do not specify a subarray, but define the index ranges of
the object to be allocated.
The []-operator generates a subarray of a ``lower'' type. For
example, if A is a nxn rmatrix, then A[i] is
the i-th row of A of type rvector
and A[i][j] is the (i,j)-th
element of A of type real.
Both types of subarray access may also be combined, for example:
A[k](i,j) is a subvector from index i to index j
of the k-th row vector of the matrix A.
The use of subarrays is illustrated in the following
example describing the LU-factorization of a nxn-matrix
A:
for (j=1; j<=n-1; j++) {
for (k=j+1; k<=n; k++) {
A[k][j] = A[k][j] / A[j][j];
A[k](j+1,n) = A[k](j+1,n) - A[k][j] * A[j](j+1,n);
}
}
This example demonstrates two important features of C-XSC. First,
we save one loop by using the subarray notation. This reduces
program complexity. Second, the program fragment above
is independent of the type of matrix A
(either rmatrix, imatrix, cmatrix or cimatrix), since all arithmetic
operators are suitably predefined in the mathematical sense.