
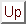

The initial value problem for a system of differential equations is to be solved by the well-known Runge-Kutta method. The C-XSC program is very similar to the mathematical notation. Dynamic vectors are used to make the program independent of the size of the system of differential equations to be solved.
Consider the first-order system of differential equations
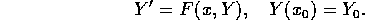
If the solution Y is known at a point x, the approximation Y(x+h) may be determined by the Runge-Kutta method:
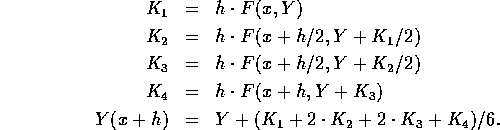
For example, we solve the system
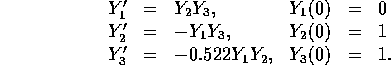
The program computes an approximation of the solution at the points
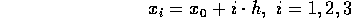
starting at given

(here:

).
#include "rvector.hpp"
rvector F(real x, rvector Y)
{ // Function definition
rvector Z(3); // Constructor call
x = 0.0; // F is independent of x
Z[1] = Y[2] * Y[3];
Z[2] = -Y[1] * Y[3];
Z[3] = -0.522 * Y[1] * Y[2];
return Z;
}
void Init(real& x, real& h, rvector& Y)
{ // Initialization
Resize(Y,3); // Resize dynamic array
x = 0.0; h = 0.1;
Y[1] = 0.0; Y[2] = 1.0; Y[3] = 1.0;
}
main()
{
real x, h; // Declarations and dynamic
rvector Y(3), K1(3), K2(3), K3(3), K4(3); // memory allocation
Init(x, h, Y);
for (int i=1; i<=3; i++) { // 3 Runge-Kutta steps
K1 = h * F(x, Y); // with array result
K2 = h * F(x + h / 2, Y + K1 / 2);
K3 = h * F(x + h / 2, Y + K2 / 2);
K4 = h * F(x + h, Y + K3);
Y = Y + (K1 + 2 * K2 + 2 * K3 + K4) / 6;
x += h;
cout << SetPrecision(18,16) << Dec; // I/O modification
cout << "Step: " << i << ", "
<< "x = " << x << endl;
cout << "Y = " << endl << Y << endl;
}
}