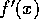 is continuous in
is continuous in 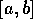 , and that
, and that


Compute an enclosure of a zero of a real
function f(x). It is assumed that the derivative 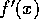 is continuous in
is continuous in 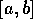 , and that
, and that
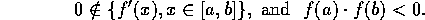
If

is an inclusion of the zero, then an improved inclusion

may be computed by
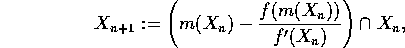
where m(X) is a point within the interval X, usually the midpoint. The mathematical theory of the Interval Newton method appears in [1].
In this example, we apply Newton's method to the function
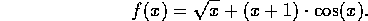
Generic function names are used for interval square root, interval sine, and interval cosine so that f may be written in a mathematical notation.
#include "interval.hpp" // Include interval arithmetic package
#include "imath.hpp" // Include interval standard functions
interval f(real& x)
{ // Function f
interval y;
y = x; // Use interval arithmetic
return sqrt(y) + (y+1.0) * cos(y);
}
interval deriv(interval& x)
{ // Derivative function f'
return (1.0 / (2.0 * sqrt(x)) + cos(x) - (x+1.0) * sin(x));
}
int criter(interval& x) // Computing: f(a)*f(b) < 0 and
{ // not 0 in f'([x])?
return ( Sup( f(Inf(x))*f(Sup(x)) ) < 0.0 && !(0.0 <= deriv(x)) );
} // '<=': `element of'
main()
{
interval y, y_old;
cout << "Please enter starting interval: "; cin >> y;
cout << SetPrecision(20,12);
if (criter(y))
do {
y_old = y;
cout << "y = " << y << endl;
y = (mid(y)-f(mid(y))/deriv(y)) & y; // Iteration formula
} while (y != y_old); // &: intersection
else
cout << "Criterion not satisfied!" << endl;
}