Example: Complex Disc Arithmetic

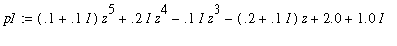
Here's the Maple Worksheet solving the task with intpakX.
> restart;
> libname:="/usr/maple/intpakX/lib", libname;
>
with(intpakX);
And this is the solution:
> A1:=[1,0,1];
![]()
> B1:=[-1,1,1];
![]()
> C1:=A1 &cmult B1;
![]()
> D1:=A1 &cmult_opt B1;
![]()
>
cmd1:=complex_disc_plot(A1,color=black):
cmd2:=complex_disc_plot(B1,color=black):
cmd3:=complex_disc_plot(C1,color=red):
cmd4:=complex_disc_plot(D1,color=blue):
> display([cmd1,cmd2,cmd3,cmd4],scaling=constrained);
![[Maple Plot]](images_compl/compl_a_e5.gif)
> p1:=(0.1+0.1*I)*z^5+0.2*I*z^4-0.1*I*z^3+(-0.2-0.1*I)*z+2.0+1.0*I;
![]()
> Z:=[-0.2,0.4,1];
![]()
> pH:=horner_eval_cent(p1,Z);
![]()
> pO:=horner_eval_opt(p1,Z);
![]()
> pC:=centred_form_eval(p1,Z);
![]()
>
cp:=complex_polynom_plot(p1,Z):
c1:=complex_disc_plot(pH,color=blue,linestyle=4):
c2:=complex_disc_plot(pO,color=green,linestyle=3):
c3:=complex_disc_plot(pC,color=black,linestyle=2):
> display([c1,c2,c3,cp],scaling=constrained);
![[Maple Plot]](images_compl/compl_a_e11.gif)
>