The following figures show resulting sets from complex operations applied to bounded rectangular regions with sides parallel to the real and imaginary axis (complex intervals). A complex interval Z=X+iY is specified by its real part interval X=[x_down, x_up] and its imaginary part interval Y=[y_down, y_up]. A point (complex number) z=x+iy is an element of such a complex interval Z if z is in Z i. e. if x_down <= x <= x_up and y_down <= y <= y_up.
For each figure the left and right hand operands Z1 and Z2, respectively as well as the operation (complex multiplication or complex division) are specified.
The arguments Z1, Z2, the resulting set Z1*Z2:= {z_1 * z_2 | ... } and the smallest complex interval enclosing Z1*Z2 are plotted. For more information about the generation of the figures consult Dorothee Miehe: "Zur Kategorisierung von Wertekomplexen bei Operationen mit Intervallen in C", Diploma Theses (supervisor W. Krämer), University of Karlsruhe, 1999.
The figures show that resulting sets from multiplication and division may be quite complicate. Wrapping the resulting sets by complex intervals lead to more or less overestimations.
The figures look fine by itself but of course the material in this note is intended to be used in courses on (complex) interval arithmetic.
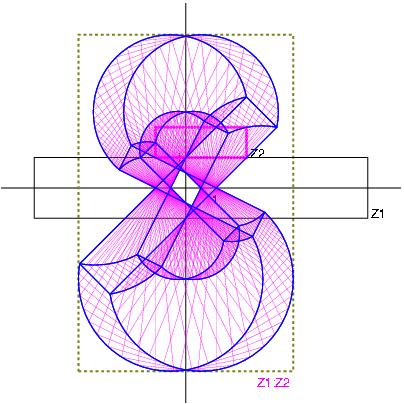
Z1*Z2 with Z1:= [-4,5] + i [-3,4] and Z2:= [-3,6] + i [1,1]
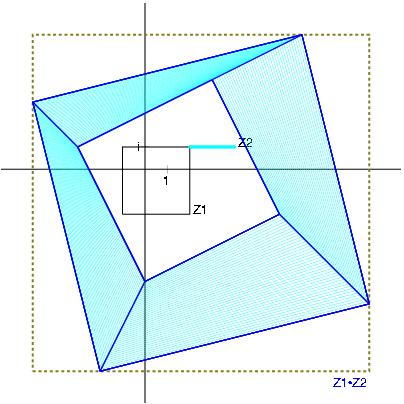
Z1*Z2 with Z1:= [-3,4] + i [-3,3] and Z2:= [1,4] + i [2,5]
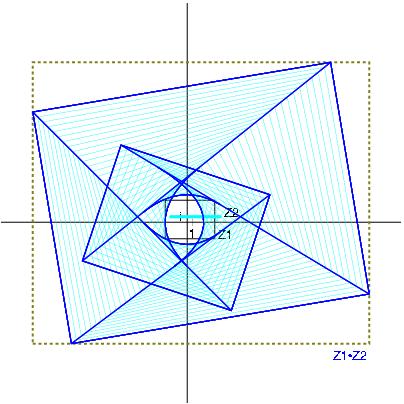
Z1*Z2 with Z1:= [-1,5] + i [2,3] and Z2:= [-6,6] + i [1,1]
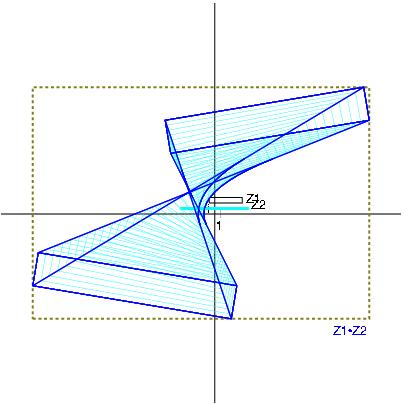
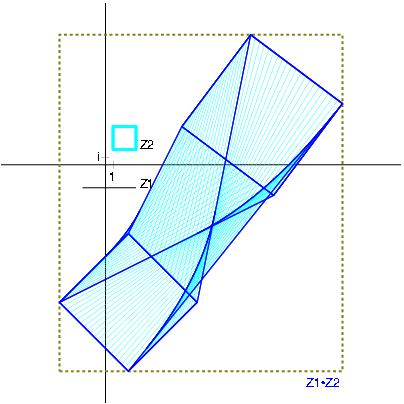
Z1*Z2 with Z1:= [-2,3] + i [-1,1] and Z2:= [-1,4] + i [-3,4]
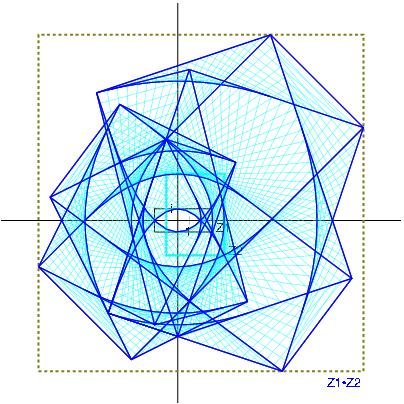
Z1*Z2 with Z1:= [-4,6] + i [1,2] and Z2:= [3,4] + i [-5,6]
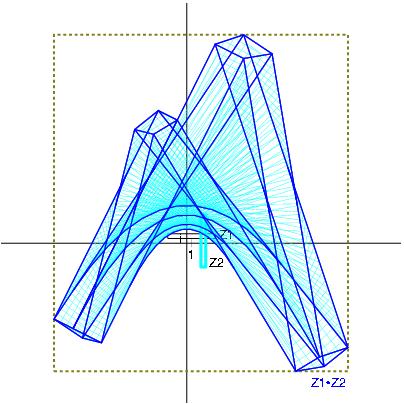
Z1*Z2 with Z1:= [-3,5] + i [-5,5] and Z2:= [1,6] + i [-2,2]
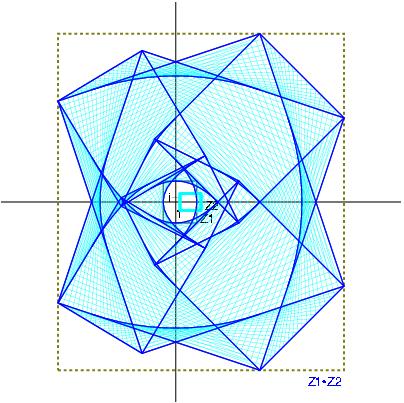
Z1*Z2 with Z1:= [-2,4] + i [-3,6] and Z2:= [-8,9] + i [1,2]
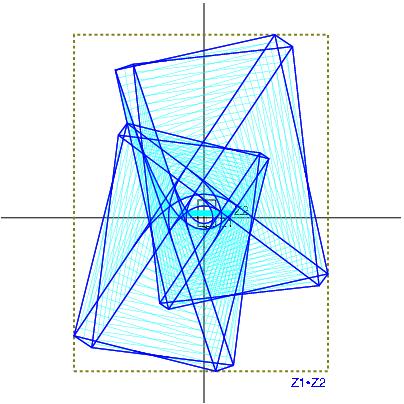
Z1*Z2 with Z1:= [1,4] + i [2,5] and Z2:= [3,5] + i [1,2]
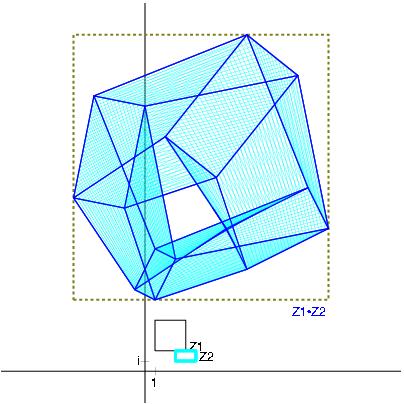
Z1*Z2 with Z1:= [-6,7] + i [1,2] and Z2:= [1,2] + i [-5,8]
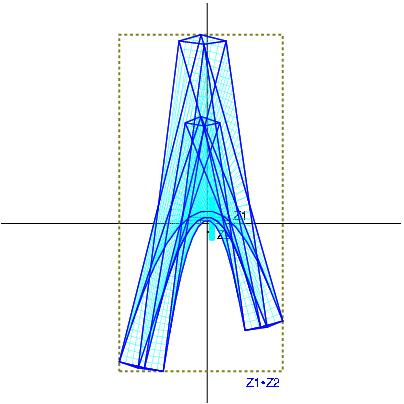
Z1 / Z2 with Z1:= [-4,6] + i [-3,5] and Z2:= [-2,3] + i [2,2]
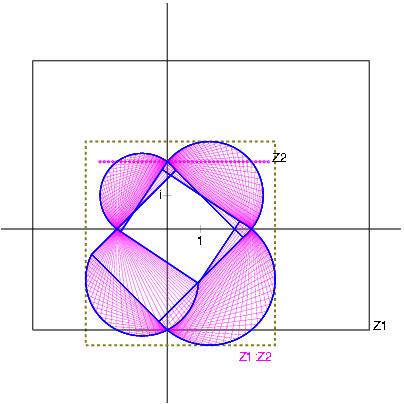
Z1 / Z2 with Z1:= [-2,3] + i [-1,5] and Z2:= [1,3] + i [1,1]
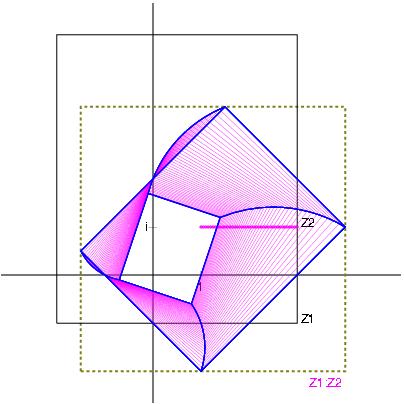
Z1 / Z2 with Z1:= [2,6] + i [4,4] and Z2:= [-1,2] + i [1,3]
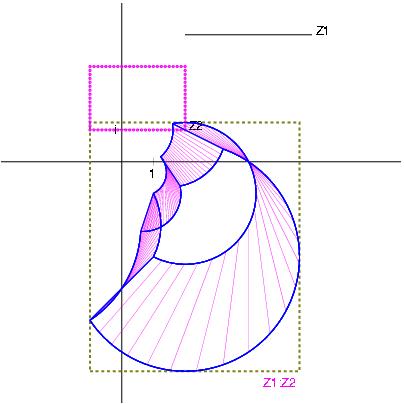
Z1 / Z2 with Z1:= [1,6] + i [2,4] and Z2:= [-3,7] + i [1,4]
Z1 / Z2 with Z1:= [-3,6] + i [2,7] and Z2:= [1,3] + i [-0.5,0.5]
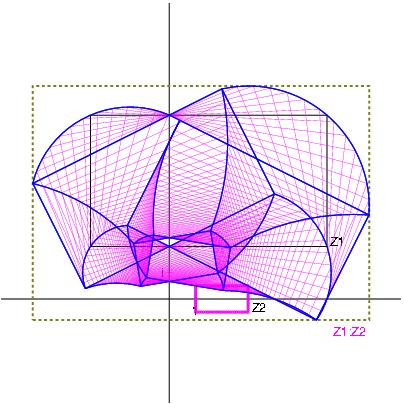
Z1 / Z2 with Z1:= [-4,5] + i [-1,6] and Z2:= [-8,9] + i [1,3]
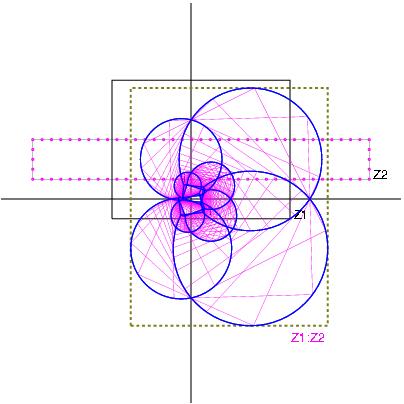
Z1 / Z2 with Z1:= [-5,6] + i [-1,1] and Z2:= [-1,2] + i [1,2]
Wiss. Rechnen / Softwaretechnologie
FB
Mathematik
Bergische
Universität Wuppertal